Najmniejsza wspólna wielokrotność (NWW) to kluczowy koncept w matematyce, który ma zastosowanie w wielu dziedzinach, od arytmetyki po bardziej złożone zagadnienia. NWW to najmniejsza liczba naturalna, która dzieli się bez reszty przez wszystkie dane liczby całkowite. Zrozumienie tego pojęcia jest istotne nie tylko w kontekście nauki matematyki, ale także w codziennym życiu, gdzie NWW pomaga w rozwiązywaniu problemów związanych z ułamkami i cyklicznością.
W artykule przyjrzymy się, jak obliczyć NWW, jakie są metody jego wyznaczania oraz w jakich sytuacjach można go zastosować. Dzięki praktycznym przykładom, każdy będzie mógł lepiej zrozumieć, jak wykorzystać NWW w różnych zadaniach matematycznych.
Najistotniejsze informacje:- NWW to najmniejsza liczba naturalna, która dzieli się bez reszty przez dane liczby całkowite.
- Obliczanie NWW jest kluczowe w znajdowaniu wspólnych mianowników ułamków.
- NWW jest używane w rozwiązywaniu równań z wielokrotnościami.
- Przykładem NWW dla liczb 6 i 8 jest 24, ponieważ dzieli się przez obie te liczby.
- Znajomość NWW pomaga w rozwiązywaniu problemów cyklicznych, takich jak planowanie wydarzeń.
Definicja NWW w matematyce i jej znaczenie dla uczniów
Najmniejsza wspólna wielokrotność (NWW) to fundamentalne pojęcie w matematyce, które odnosi się do najmniejszej liczby naturalnej, dzielącej się bez reszty przez dane liczby całkowite. Zrozumienie NWW jest kluczowe dla uczniów, ponieważ pozwala im na lepsze radzenie sobie z problemami matematycznymi, takimi jak obliczanie wspólnych mianowników ułamków. NWW jest nie tylko teoretycznym konceptem, ale również praktycznym narzędziem, które znajduje zastosowanie w różnych sytuacjach życiowych.
Znajomość NWW ma ogromne znaczenie w edukacji matematycznej. Pomaga uczniom rozwijać umiejętności logicznego myślenia oraz rozwiązywania problemów. W codziennym życiu, NWW może być używane w zadaniach dotyczących cykliczności, takich jak planowanie wydarzeń czy organizowanie zajęć. Przykładowo, uczniowie mogą wykorzystać NWW, aby zrozumieć, jak harmonizować różne terminy lub cykle, co jest niezwykle przydatne w ich codziennych obowiązkach.
Czym jest najmniejsza wspólna wielokrotność i jak ją zrozumieć?
NWW to liczba, która jest najmniejszą wspólną wielokrotnością dla zestawu liczb. Na przykład, dla liczb 4 i 6, NWW wynosi 12, ponieważ 12 jest najmniejszą liczbą, która dzieli się bez reszty przez obie te liczby. Zrozumienie tego pojęcia wymaga znajomości pojęcia wielokrotności oraz umiejętności identyfikacji najmniejszych wspólnych wartości. NWW jest istotne w kontekście wielu działań matematycznych, w tym obliczania ułamków i rozwiązywania równań.
- NWW dla liczb 8 i 12 to 24, ponieważ 24 jest najmniejszą liczbą dzielącą się przez obie.
- Dla liczb 15 i 20, NWW wynosi 60, co pokazuje, jak ważne jest zrozumienie tego konceptu w praktycznych obliczeniach.
- Wielokrotności liczb są podstawą do wyznaczania NWW, co czyni je kluczowym elementem w nauce matematyki.
Dlaczego NWW jest istotne w matematyce i codziennym życiu?
Najmniejsza wspólna wielokrotność (NWW) odgrywa kluczową rolę w rozwiązywaniu wielu problemów matematycznych oraz w codziennych sytuacjach. Zrozumienie NWW pozwala uczniom na łatwiejsze znajdowanie wspólnych mianowników ułamków, co jest niezbędne w bardziej zaawansowanych obliczeniach. W życiu codziennym NWW jest przydatne w organizacji czasu, na przykład podczas planowania spotkań, gdzie różne terminy muszą być zsynchronizowane. Dzięki NWW można również efektywnie dzielić zasoby, takie jak jedzenie czy materiały, aby zaspokoić potrzeby grupy.
NWW ma zastosowanie nie tylko w matematyce, ale także w innych dziedzinach. Na przykład, w inżynierii i technologii, NWW jest wykorzystywane do synchronizacji cykli pracy maszyn. Warto zauważyć, że znajomość NWW może pomóc w codziennych zadaniach, takich jak planowanie zakupów czy organizowanie zajęć w szkole. Umożliwia to lepsze zarządzanie czasem i zasobami, co jest niezwykle ważne w dzisiejszym szybkim świecie.
Jak obliczyć NWW dla różnych liczb i zastosowania
Aby skutecznie obliczyć NWW, istnieje kilka metod, które można zastosować w zależności od dostępnych informacji. Jedną z najpopularniejszych metod jest metoda rozkładu na czynniki pierwsze, która polega na rozłożeniu każdej z liczb na czynniki pierwsze, a następnie wybraniu największej potęgi każdego czynnika pojawiającego się w rozkładzie. Na przykład, dla liczb 12 i 15, rozkłady to 2² × 3¹ i 3¹ × 5¹. W takim przypadku NWW wynosi 2² × 3¹ × 5¹ = 60.
Inną metodą jest metoda wyliczania wielokrotności, która polega na wypisaniu wielokrotności danej liczby, aż znajdziemy najmniejszą wspólną wartość. Na przykład, dla 4 i 6, wielokrotności 4 to 4, 8, 12, 16, a dla 6 to 6, 12, 18. Najmniejszą wspólną wielokrotnością jest 12. Obie metody są efektywne, jednak wybór metody zależy od preferencji oraz kontekstu problemu matematycznego.
Metody obliczania NWW: przykłady krok po kroku
Aby obliczyć najmniejszą wspólną wielokrotność (NWW), można zastosować metodę rozkładu na czynniki pierwsze. Ta metoda polega na rozłożeniu każdej z liczb na czynniki pierwsze, a następnie wybraniu największej potęgi każdego czynnika, który pojawia się w rozkładzie. Na przykład, dla liczb 12 i 15, rozkład na czynniki pierwsze wygląda następująco: 12 = 2² × 3¹, a 15 = 3¹ × 5¹. Następnie, aby znaleźć NWW, bierzemy każdy czynnik z najwyższą potęgą, co daje nam 2² × 3¹ × 5¹ = 60.
Przykład krok po kroku dla liczb 12 i 15:
- Rozłóż 12 na czynniki: 12 = 2² × 3¹.
- Rozłóż 15 na czynniki: 15 = 3¹ × 5¹.
- Wybierz największe potęgi czynników: 2² (z 12), 3¹ (w obu), 5¹ (z 15).
- Pomnóż te największe potęgi: 2² × 3¹ × 5¹ = 4 × 3 × 5 = 60.
- NWW dla 4 i 6 to 12.
- NWW dla 8 i 12 to 24.
- NWW dla 10 i 15 to 30.
Zastosowanie NWW w znajdowaniu wspólnych mianowników ułamków
W praktyce, NWW jest niezwykle przydatne w znajdowaniu wspólnych mianowników dla ułamków. Aby dodać lub odjąć ułamki, muszą one mieć ten sam mianownik. NWW pozwala na szybkie ustalenie, jaki mianownik będzie wspólny dla różnych ułamków. Na przykład, aby dodać ułamki 1/4 i 1/6, najpierw musimy znaleźć NWW dla 4 i 6, które wynosi 12. Następnie przekształcamy ułamki tak, aby miały wspólny mianownik: 1/4 = 3/12 i 1/6 = 2/12. Teraz możemy łatwo dodać te ułamki: 3/12 + 2/12 = 5/12.
Inny przykład to ułamki 2/3 i 1/5. Najpierw znajdujemy NWW dla 3 i 5, co daje 15. Następnie przekształcamy ułamki: 2/3 = 10/15 i 1/5 = 3/15. Po przekształceniu możemy dodać: 10/15 + 3/15 = 13/15. Dzięki zastosowaniu NWW, proces dodawania ułamków staje się znacznie prostszy i bardziej zrozumiały.
Praktyczne przykłady z wykorzystaniem NWW w zadaniach
Najmniejsza wspólna wielokrotność (NWW) znajduje zastosowanie w wielu praktycznych sytuacjach, które pomagają w rozwiązywaniu problemów matematycznych. Na przykład, w zadaniach dotyczących harmonogramów, NWW może być używane do ustalania wspólnych terminów dla różnych wydarzeń. Jeśli mamy dwa wydarzenia, które odbywają się co 4 dni i co 6 dni, NWW dla tych liczb wynosi 12. Oznacza to, że oba wydarzenia będą miały miejsce w tym samym dniu po 12 dniach. Tego rodzaju zastosowanie NWW jest nieocenione w codziennym planowaniu i organizacji czasu.
Czytaj więcej: Ile kosztuje Louis Vuitton Neverfull? Poznaj ceny i modele torebek
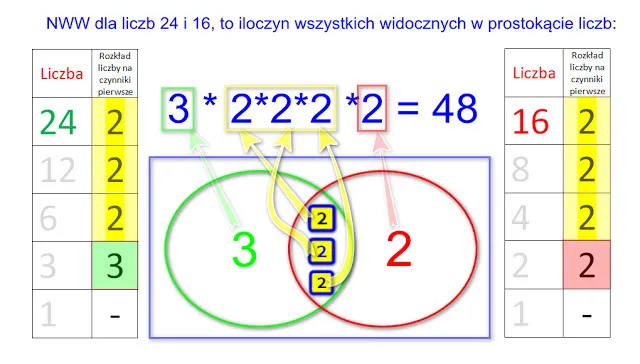
Kolejnym przykładem może być sytuacja, w której musimy podzielić zasoby, takie jak jedzenie lub materiały, pomiędzy grupy osób. Załóżmy, że mamy 8 jabłek i 12 pomarańczy, a chcemy podzielić je równo pomiędzy grupę dzieci. Aby ustalić, ile owoców dostanie każda osoba, należy znaleźć NWW dla 8 i 12, które wynosi 24. Dzięki temu możemy zorganizować podział tak, aby każda osoba otrzymała równą ilość owoców, co jest kluczowe w sytuacjach, gdy sprawiedliwość w podziale jest istotna.
Rozwiązywanie równań z wielokrotnościami za pomocą NWW
Rozwiązywanie równań z wielokrotnościami za pomocą NWW jest skuteczną metodą, która ułatwia obliczenia. Na przykład, rozważmy równanie 2x + 3 = 11. Aby znaleźć wartość x, najpierw przekształcamy równanie, odejmując 3 od obu stron, co daje nam 2x = 8. Następnie dzielimy obie strony przez 2, uzyskując x = 4. W tym przypadku użycie NWW nie jest bezpośrednio potrzebne, ale w bardziej złożonych równaniach z wielokrotnościami, takich jak 3x + 4 = 2x + 10, możemy użyć NWW dla 3 i 2, aby ustalić wspólne wartości, co ułatwi dalsze obliczenia. Zastosowanie NWW w takich zadaniach pozwala na uproszczenie procesu rozwiązywania równań i lepsze zrozumienie relacji między zmiennymi.
NWW w kontekście cykliczności i problemów praktycznych
Najmniejsza wspólna wielokrotność (NWW) jest niezwykle przydatna w rozwiązywaniu problemów cyklicznych, które występują w codziennym życiu. Na przykład, jeśli mamy dwa różne wydarzenia, które odbywają się w różnych odstępach czasu, NWW pozwala nam ustalić, kiedy oba wydarzenia będą miały miejsce jednocześnie. Wyobraźmy sobie, że jedno wydarzenie odbywa się co 3 dni, a drugie co 4 dni. NWW dla tych dwóch liczb wynosi 12, co oznacza, że oba wydarzenia zbiegają się w tym samym dniu co 12 dni. Tego rodzaju zastosowanie NWW jest przydatne w planowaniu spotkań, zajęć czy innych cyklicznych aktywności.
Innym przykładem może być synchronizacja pracy maszyn w zakładzie produkcyjnym. Jeśli maszyna A działa co 6 godzin, a maszyna B co 8 godzin, NWW dla tych cykli wynosi 24 godziny. Oznacza to, że co 24 godziny obie maszyny będą pracować jednocześnie. W takich przypadkach, NWW pomaga w optymalizacji procesów produkcyjnych, co prowadzi do zwiększenia efektywności i oszczędności czasu.
| Problem | NWW | Opis |
|---|---|---|
| Spotkania co 3 i 4 dni | 12 | Oba wydarzenia będą miały miejsce jednocześnie co 12 dni. |
| Maszyna A co 6 godzin i maszyna B co 8 godzin | 24 | Obie maszyny będą pracować razem co 24 godziny. |
| Tramwaj kursujący co 10 minut i autobus co 15 minut | 30 | Oba środki transportu będą na przystanku jednocześnie co 30 minut. |
Wykorzystanie NWW w optymalizacji procesów produkcyjnych
Najmniejsza wspólna wielokrotność (NWW) ma ogromny potencjał w optymalizacji procesów produkcyjnych, zwłaszcza w kontekście automatyzacji i zarządzania czasem pracy maszyn. W miarę jak przemysł 4.0 zyskuje na znaczeniu, przedsiębiorstwa mogą korzystać z NWW do synchronizacji cykli pracy różnych maszyn, co prowadzi do zwiększenia wydajności. Przykładowo, przy zastosowaniu NWW, można zharmonizować pracę maszyn, aby minimalizować czas przestoju i maksymalizować produkcję. Dzięki temu możliwe jest lepsze planowanie konserwacji oraz serwisowania urządzeń, co z kolei obniża koszty operacyjne.
Co więcej, wykorzystanie NWW w analizie danych produkcyjnych może pomóc w identyfikacji wzorców oraz optymalizacji harmonogramów pracy. Zastosowanie zaawansowanych algorytmów analitycznych, które uwzględniają NWW, może prowadzić do bardziej efektywnego zarządzania zasobami i lepszego dostosowania produkcji do zmieniających się potrzeb rynku. W efekcie, przedsiębiorstwa mogą zwiększać swoją konkurencyjność, dostosowując się do dynamicznych warunków rynkowych.
