Obliczanie sinusa kąta jest kluczowym zagadnieniem w matematyce, szczególnie w geometrii i trygonometrii. Istnieje wiele metod, które umożliwiają uzyskanie wartości sinusa, a wybór odpowiedniej zależy od dostępnych narzędzi i danych. W tym artykule przedstawimy najpopularniejsze sposoby obliczania sinusa, w tym wykorzystanie trójkątów prostokątnych, kalkulatorów, tablic trygonometrycznych oraz bardziej zaawansowane metody, takie jak szereg Taylora.
Bez względu na to, czy jesteś uczniem, studentem, czy osobą pracującą w branży technicznej, zrozumienie, jak obliczyć sinus, jest niezwykle przydatne. Dzięki prostym przykładom i jasnym instrukcjom, każdy będzie mógł skutecznie obliczać sinus kąta.
Najważniejsze informacje:- Sinus kąta w trójkącie prostokątnym to stosunek długości przyprostokątnej naprzeciwległej do kąta do długości przeciwprostokątnej.
- Można obliczyć sinus za pomocą kalkulatora, upewniając się, że jest ustawiony na odpowiednią jednostkę miary.
- Tablice trygonometryczne zawierają wartości sinusa dla standardowych kątów, co ułatwia szybkie obliczenia.
- Szereg Taylora pozwala na przybliżenie wartości sinusa dla kątów w radianach.
- Praktyczne zastosowanie sinusa występuje w wielu dziedzinach, takich jak inżynieria i architektura.
Jak obliczyć sinus kąta w trójkątnym prostokątnym dla początkujących
Sinus kąta to jedna z podstawowych funkcji trygonometrycznych, która odgrywa kluczową rolę w geometrii, zwłaszcza w kontekście trójkątów prostokątnych. Definiuje się go jako stosunek długości przyprostokątnej naprzeciwległej do kąta do długości przeciwprostokątnej. Wzór na sinus wygląda następująco: $$\sin(\theta) = \frac{a}{c}$$, gdzie $a$ to długość przyprostokątnej, a $c$ to długość przeciwprostokątnej. Zrozumienie tej definicji jest fundamentalne, ponieważ pozwala na obliczanie wartości sinusa i zastosowanie go w różnych zadaniach matematycznych.
Sinus jest szczególnie użyteczny w przypadku trójkątów prostokątnych, gdzie jeden z kątów wynosi 90 stopni. Dzięki tej funkcji możemy łatwo określić relacje między kątami a długościami boków trójkąta. Na przykład, jeśli mamy trójkąt prostokątny z kątem 30 stopni, możemy obliczyć sinus tego kąta, co pozwoli nam znaleźć długość przeciwprostokątnej w stosunku do długości przyprostokątnej. W ten sposób sinus staje się narzędziem do rozwiązywania wielu problemów geometrycznych i trygonometrycznych.
Zrozumienie definicji sinusa i jego zastosowania w geometrii
Definicja sinusa jest kluczowa w zrozumieniu jego zastosowań w geometrii. Sinus kąta ostrego w trójkącie prostokątnym jest używany do obliczeń związanych z długościami boków oraz kątami. Dzięki tej funkcji możemy określić, jak zmieniają się długości boków w zależności od wartości kąta. Sinus jest także niezbędny w wielu dziedzinach, takich jak inżynieria, architektura czy fizyka, gdzie precyzyjne obliczenia kątów i wymiarów są niezwykle ważne. Jego zrozumienie jest więc fundamentem dla wszystkich, którzy chcą zgłębiać tajniki matematyki i jej zastosowania w praktyce.
Przykład obliczania sinusa w praktycznym trójkącie prostokątnym
Aby lepiej zrozumieć, jak obliczyć sinus, przyjrzyjmy się konkretnemu przykładowi. Rozważmy trójkąt prostokątny, w którym długość przyprostokątnej naprzeciwległej do kąta wynosi 3 cm, a długość przeciwprostokątnej to 5 cm. Aby obliczyć sinus kąta, używamy wzoru: $$\sin(\theta) = \frac{a}{c}$$, gdzie $a$ to długość przyprostokątnej, a $c$ to długość przeciwprostokątnej. W naszym przypadku obliczenia będą wyglądały następująco: $$\sin(\theta) = \frac{3}{5} = 0,6$$.
Oznacza to, że sinus kąta w tym trójkącie prostokątnym wynosi 0,6. Taki wynik pozwala na dalsze obliczenia, na przykład w celu określenia innych kątów lub długości boków w tym trójkącie. Dzięki temu przykładowi można zauważyć, jak praktyczne zastosowanie ma funkcja sinus w geometrii i jak łatwo można ją obliczyć przy pomocy prostych danych.
Metody obliczania sinusa: narzędzia i techniki dla każdego
Obliczanie sinusa można przeprowadzać na wiele sposobów. Jednym z najpopularniejszych narzędzi jest kalkulator, który umożliwia szybkie i łatwe uzyskanie wartości sinusa dla dowolnego kąta. Aby skorzystać z kalkulatora, należy upewnić się, że jest on ustawiony na odpowiednią jednostkę miary, czyli stopnie lub radiany. Następnie wystarczy wpisać wartość kąta i nacisnąć przycisk "sin". To szybkie podejście sprawia, że obliczenia stają się bardziej dostępne dla każdego, niezależnie od poziomu zaawansowania w matematyce.
Czytaj więcej: Które lotnisko w Paryżu jest najbliżej centrum i jak tam dojechać?
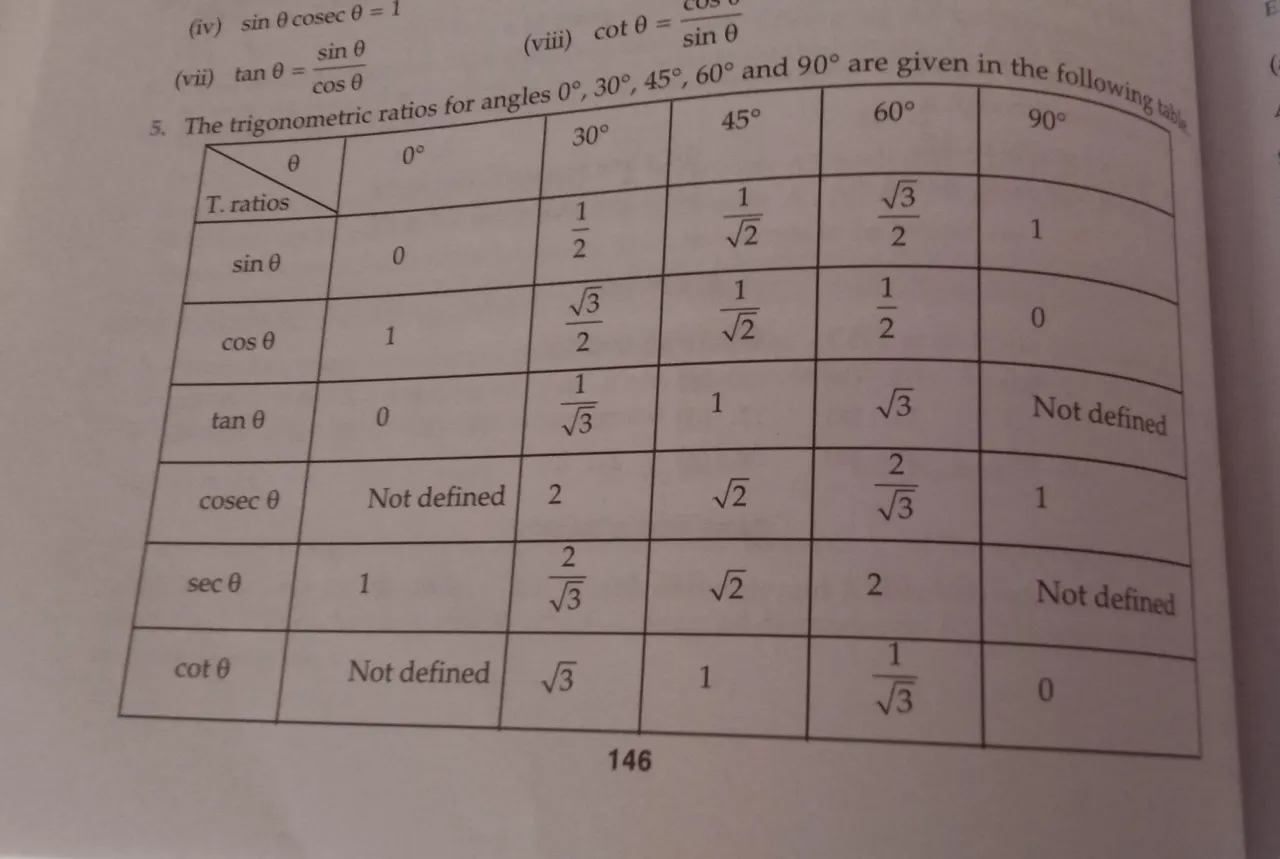
Kolejną przydatną metodą są tablice trygonometryczne, które zawierają wartości sinusa dla standardowych kątów, takich jak 30°, 45° czy 60°. Korzystając z tych tablic, można szybko znaleźć wartość sinusa bez potrzeby wykonywania obliczeń. Wystarczy odszukać odpowiedni kąt w tabeli, co jest szczególnie przydatne w sytuacjach, gdy potrzebujemy szybkich wyników, na przykład w czasie egzaminów lub podczas rozwiązywania zadań domowych.
Użycie kalkulatora do obliczenia wartości sinusa z kąta
Aby obliczyć sinus kąta za pomocą kalkulatora, należy najpierw upewnić się, że urządzenie jest ustawione na odpowiednią jednostkę miary: stopnie lub radiany. Następnie, wprowadź wartość kąta, dla którego chcesz znaleźć sinus. Po wpisaniu wartości, wystarczy nacisnąć przycisk oznaczony jako "sin" lub "sinus". Kalkulator natychmiast wyświetli wynik, który będzie wartością sinusa dla podanego kąta. To szybka i efektywna metoda, która jest szczególnie przydatna w sytuacjach, gdy potrzebujesz szybkich obliczeń.
Jak wykorzystać tablice trygonometryczne do szybkiego obliczenia
Tablice trygonometryczne to doskonałe narzędzie do szybkiego znajdowania wartości sinusa dla standardowych kątów, takich jak 0°, 30°, 45°, 60° i 90°. Aby z nich skorzystać, wystarczy znaleźć odpowiedni kąt w tabeli, a obok niego znajduje się wartość sinusa. Na przykład, dla kąta 30° wartość sinusa wynosi 0,5, a dla kąta 45° wynosi 0,707. Dzięki tablicom można szybko uzyskać potrzebne wyniki bez potrzeby skomplikowanych obliczeń, co czyni je przydatnym narzędziem w edukacji matematycznej oraz w codziennych zastosowaniach.
Jak obliczyć sinus za pomocą szeregu Taylora dla zaawansowanych
Szereg Taylora to potężne narzędzie matematyczne, które pozwala na przybliżenie funkcji, w tym funkcji sinus. Dla funkcji sinus, rozwinięcie w szereg Taylora w punkcie 0 (tzw. rozwinięcie Maclaurina) można zapisać jako: $$\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \ldots$$. Oznacza to, że sinus kąta można obliczyć, sumując kolejne składniki tego szeregu, co daje coraz dokładniejsze przybliżenia. Im więcej składników uwzględnimy, tym dokładniejszy będzie wynik.
Na przykład, aby obliczyć sinus kąta 1 radiana, możemy użyć pierwszych trzech składników szeregu Taylora. Obliczenia będą wyglądały następująco: $$\sin(1) \approx 1 - \frac{1^3}{6} + \frac{1^5}{120} = 1 - 0,1667 + 0,0083 \approx 0,8416$$. To przybliżenie jest bliskie rzeczywistej wartości sinusa dla 1 radiana, która wynosi około 0,8415. Wykorzystanie szeregu Taylora jest szczególnie przydatne w sytuacjach, gdy potrzebujemy obliczyć sinus dla wartości, które nie są łatwe do wyznaczenia za pomocą standardowych metod.
Przykłady obliczeń sinusa przy użyciu szeregu Taylora
Przykładem obliczenia sinusa przy użyciu szeregu Taylora może być obliczenie wartości sinusa dla kąta 0,5 radiana. Używając rozwinięcia, mamy: $$\sin(0.5) \approx 0.5 - \frac{0.5^3}{6} + \frac{0.5^5}{120}$$. Obliczając to krok po kroku, otrzymujemy: $$\sin(0.5) \approx 0.5 - \frac{0.125}{6} + \frac{0.03125}{120} = 0.5 - 0.020833 + 0.0002604 \approx 0.479425$$. To przybliżenie jest zbliżone do rzeczywistej wartości sinusa dla 0,5 radiana, która wynosi około 0,479426. Takie podejście pokazuje, jak przydatny jest szereg Taylora w obliczeniach trygonometrycznych.
Zastosowanie sinusa w praktyce: przykłady z życia codziennego
Sinus odgrywa kluczową rolę w wielu dziedzinach inżynierii, gdzie jest wykorzystywany do obliczeń związanych z kątami i długościami. Na przykład, w inżynierii mechanicznej, sinus jest używany do obliczania sił działających na elementy konstrukcyjne, takie jak dźwignie czy belki. Dzięki funkcji sinus inżynierowie mogą określić, jak różne kąty wpływają na stabilność i wytrzymałość konstrukcji. Ponadto, w projektowaniu systemów hydraulicznych, sinus pomaga w określaniu przepływu cieczy w rurach pod różnymi kątami, co jest kluczowe dla efektywności systemu.
W architekturze, sinus jest również niezwykle istotny, szczególnie przy projektowaniu budynków i innych struktur. Używa się go do obliczania wysokości budynków w oparciu o kąt nachylenia dachu czy też do określenia odpowiednich proporcji w projektach. Na przykład, architekci mogą wykorzystać sinus do zaprojektowania schodów, aby upewnić się, że mają one odpowiedni kąt nachylenia, co wpływa na komfort użytkowania. Dodatkowo, sinus jest pomocny w analizie oświetlenia naturalnego w pomieszczeniach, co pozwala na lepsze wykorzystanie światła słonecznego.
- Obliczenia sił w inżynierii mechanicznej przy użyciu funkcji sinus.
- Projektowanie systemów hydraulicznych z uwzględnieniem kątów przepływu.
- Obliczanie wysokości budynków na podstawie kątów nachylenia dachów.
- Ustalanie proporcji w projektach architektonicznych dla lepszego komfortu użytkowania.
- Analiza oświetlenia naturalnego w pomieszczeniach dla efektywności energetycznej.
Sinus w inżynierii i architekturze: jak to działa?
W inżynierii, sinus jest wykorzystywany do obliczeń dotyczących kątów i sił. Na przykład, w projektowaniu mostów, inżynierowie muszą obliczyć siły działające na różne elementy konstrukcyjne, aby zapewnić ich stabilność. Sinus pomaga w określeniu, jak różne kąty wpływają na obciążenie mostu. W architekturze, sinus jest używany do projektowania schodów oraz dachów, gdzie odpowiednie kąty są kluczowe dla funkcjonalności i estetyki budynku. Przykładem może być projekt nowoczesnego budynku, gdzie architekci używają funkcji sinus do obliczenia odpowiednich kątów nachylenia dachu, co pozwala na efektywne odprowadzanie wody deszczowej.
Jak sinus wpływa na nowoczesne technologie i innowacje
W miarę jak technologia się rozwija, zastosowanie funkcji sinus staje się coraz bardziej złożone i innowacyjne. Na przykład, w technologii obrazowania, sinus jest wykorzystywany w algorytmach przetwarzania sygnałów, które umożliwiają poprawę jakości obrazów w medycynie, takich jak tomografia komputerowa czy rezonans magnetyczny. Dzięki zastosowaniu funkcji sinus w analizie częstotliwości, lekarze mogą uzyskać bardziej precyzyjne obrazy, co prowadzi do lepszej diagnozy i leczenia pacjentów.
Dodatkowo, w robotyce i automatyce, sinus jest kluczowy w programowaniu ruchu robotów. Wykorzystując funkcje sinusowe, inżynierowie mogą precyzyjnie kontrolować trajektorie ruchu robotów, co jest niezbędne w zastosowaniach przemysłowych oraz w medycynie, gdzie roboty chirurgiczne muszą działać z najwyższą precyzją. Przyszłość może przynieść jeszcze więcej zastosowań sinusa w dziedzinach takich jak sztuczna inteligencja i uczenie maszynowe, gdzie funkcje sinusowe mogą być używane do modelowania złożonych danych i przewidywania trendów w różnych branżach.

