Wierzchołki to kluczowe pojęcie w matematyce, które odnosi się do punktów, w których przecinają się linie lub krawędzie. W kontekście geometrycznym, wierzchołek jest miejscem, gdzie spotykają się dwie lub więcej prostych, a jego zrozumienie jest niezbędne do analizy różnych kształtów, zarówno dwuwymiarowych, jak i trójwymiarowych. Na przykład, każdy trójkąt ma trzy wierzchołki, które definiują jego formę, podczas gdy kwadrat ma ich cztery. Zrozumienie, jak wierzchołki wpływają na kształty, jest kluczowe dla dalszego zgłębiania matematyki.
Wierzchołki nie tylko odgrywają istotną rolę w geometrii, ale także w algebrze i teorii grafów. W przypadku parabol, na przykład, wierzchołek to punkt, w którym funkcja osiąga swoje maksimum lub minimum. W teorii grafów, wierzchołki są podstawowymi elementami, które łączą się krawędziami, tworząc złożone struktury. W niniejszym artykule przyjrzymy się bliżej definicji wierzchołków, ich zastosowaniom oraz ich znaczeniu w różnych dziedzinach matematyki.
Kluczowe informacje:- Wierzchołek to punkt, w którym przecinają się dwie lub więcej linii lub krawędzi.
- Każdy kształt geometryczny, taki jak trójkąt czy kwadrat, ma swoje wierzchołki, które definiują jego strukturę.
- Nie wszystkie kształty mają wierzchołki; na przykład koła i owale ich nie posiadają.
- W trójwymiarowych obiektach, takich jak sześcian, wierzchołki są miejscami, gdzie spotykają się krawędzie.
- W teorii grafów, wierzchołki są kluczowymi elementami, które łączą się krawędziami, tworząc różne struktury.
- W algebrze, parabola ma jeden wierzchołek, który jest istotny dla analizy jej zachowania.
Definicja wierzchołków w matematyce i ich znaczenie
W matematyce, wierzchołek to punkt, w którym przecinają się dwie lub więcej linii lub krawędzi. To fundamentalne pojęcie, które odgrywa kluczową rolę w geometrii oraz algebrze. Wierzchołki są niezbędne do zrozumienia struktury różnych kształtów, zarówno dwuwymiarowych, jak i trójwymiarowych. Na przykład, w przypadku trójkąta, wierzchołki definiują jego formę i kształt, a w przypadku kwadratu, są to cztery narożniki. Zrozumienie wierzchołków pozwala na głębsze zrozumienie relacji między różnymi elementami w matematyce.
W kontekście geometrii, wierzchołki mają ogromne znaczenie, ponieważ pomagają określić kształt i właściwości figur geometrycznych. W algebrze, wierzchołki pojawiają się w kontekście wykresów funkcji, gdzie reprezentują kluczowe punkty, takie jak maksimum czy minimum. Warto zauważyć, że nie wszystkie kształty mają wierzchołki; na przykład koła nie mają żadnych narożników, co czyni je wyjątkowymi w porównaniu do innych figur. Dlatego wierzchołki są nie tylko podstawowym elementem w geometrii, ale również kluczowym pojęciem w różnych dziedzinach matematyki.
Wierzchołki w geometrii: Kluczowe pojęcie dla zrozumienia kształtów
W geometrii wierzchołki odgrywają kluczową rolę w definiowaniu kształtów. Każdy kształt dwuwymiarowy, taki jak trójkąt, kwadrat czy prostokąt, składa się z wierzchołków, które są punktami, w których krawędzie się spotykają. Na przykład, trójkąt ma trzy wierzchołki, a każdy z nich jest miejscem, gdzie spotykają się dwie krawędzie. Te wierzchołki są ważne, ponieważ pomagają określić, jak kształt wygląda i jakie ma właściwości, takie jak symetria czy pole powierzchni.
W przypadku czworokątów, takich jak kwadrat czy prostokąt, wierzchołki również odgrywają istotną rolę. Kwadrat ma cztery wierzchołki, które są jego narożnikami, a każdy z tych punktów jest kluczowy dla zrozumienia jego struktury. Warto zauważyć, że niektóre figury, takie jak okrąg czy elipsa, nie mają wierzchołków, ponieważ są to kształty gładkie bez ostrych krawędzi. To pokazuje, jak różnorodne mogą być kształty w geometrii i jak wierzchołki wpływają na ich definicję.
- Trójkąt ma 3 wierzchołki, które są jego kluczowymi punktami.
- Kwadrat składa się z 4 wierzchołków, które definiują jego kształt.
- Okrąg nie ma wierzchołków, ponieważ jest gładki i nie ma narożników.
Przykłady wierzchołków w kształtach dwuwymiarowych i ich zastosowania
Wierzchołki są kluczowymi elementami w różnych dwuwymiarowych kształtach, a ich zrozumienie jest niezbędne do analizy tych figur. Na przykład, trójkąt składa się z trzech wierzchołków, które są miejscami, w których spotykają się jego krawędzie. Każdy z tych wierzchołków jest istotny, ponieważ definiuje kształt trójkąta i jego właściwości, takie jak pole powierzchni czy obwód. W praktyce, wierzchołki trójkąta mogą być wykorzystywane w architekturze do projektowania stabilnych konstrukcji, które opierają się na zasadach geometrycznych.
Kolejnym przykładem jest kwadrat, który ma cztery wierzchołki. Te wierzchołki są kluczowe dla zrozumienia symetrii i równych boków kwadratu. W zastosowaniach praktycznych, kwadraty są często używane w planowaniu przestrzennym, na przykład w projektowaniu układów ulic czy w architekturze. Pentagon, z pięcioma wierzchołkami, również ma swoje zastosowania, zwłaszcza w geometrii i grafice komputerowej, gdzie wierzchołki definiują kształt obiektów w przestrzeni cyfrowej. Warto zauważyć, że w przypadku niektórych kształtów, takich jak okrąg, nie występują wierzchołki, co czyni je wyjątkowymi w porównaniu do innych figur.
Czytaj więcej: Bretończycy: Odkryj ich bogatą kulturę i tradycje w Bretanii
- Trójkąt ma 3 wierzchołki, które są kluczowe dla jego struktury.
- Kwadrat składa się z 4 wierzchołków, co definiuje jego symetrię.
- Pentagon ma 5 wierzchołków, używanych w różnych zastosowaniach graficznych.
Wierzchołki w trójwymiarowych obiektach i ich właściwości
Wierzchołki w obiektach trójwymiarowych różnią się od tych w dwuwymiarowych kształtach, ponieważ odgrywają kluczową rolę w definiowaniu struktury brył. Na przykład, w przypadku sześcianu, który ma osiem wierzchołków, każdy z nich jest punktem, w którym spotykają się trzy krawędzie. Wierzchołki są istotne dla stabilności obiektów, ponieważ pomagają w utrzymaniu ich kształtu i symetrii. W obiektach takich jak piramida, wierzchołki są kluczowe dla określenia jej charakterystyki, a ich rozmieszczenie wpływa na równowagę całej struktury. W przeciwieństwie do tego, sfera nie ma wierzchołków, ponieważ jest gładka i nie ma ostrych krawędzi, co czyni ją unikalną w porównaniu do innych trójwymiarowych form.
| Kształt | Liczba wierzchołków |
|---|---|
| Sześcian | 8 |
| Tetrahedron | 4 |
| Okthedron | 6 |
| Piramida | 5 |
| Walc | 2 |
Jak wierzchołki wpływają na strukturę brył i ich charakterystyki
Wierzchołki mają istotny wpływ na stabilność oraz symetrię trójwymiarowych kształtów. Na przykład, w sześcianie, każdy z ośmiu wierzchołków odgrywa kluczową rolę w utrzymaniu jego symetrii i równowagi. W przypadku piramidy, wierzchołek na szczycie jest kluczowy dla jej kształtu, a rozmieszczenie pozostałych wierzchołków wpływa na stabilność całej konstrukcji. W praktyce, architekci i inżynierowie wykorzystują te zasady, aby projektować budynki i inne struktury, które są zarówno estetyczne, jak i funkcjonalne.
Warto również zauważyć, że wierzchołki wpływają na sposób, w jaki światło odbija się od powierzchni brył. Na przykład, w przypadku obiektów takich jak diamenty, odpowiednie rozmieszczenie wierzchołków jest kluczowe dla uzyskania efektu załamania światła, co zwiększa ich blask. Zrozumienie, jak wierzchołki wpływają na właściwości brył, jest istotne nie tylko w matematyce, ale także w dziedzinach takich jak fizyka czy inżynieria.

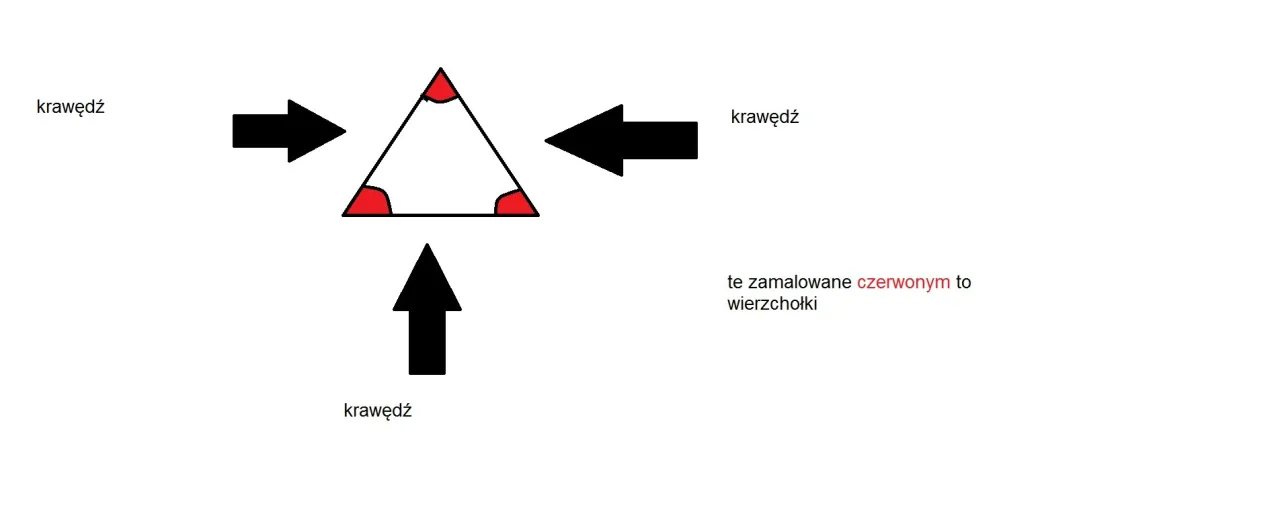
Rola wierzchołków w teorii grafów i ich zastosowania
W teorii grafów, wierzchołki są podstawowymi elementami, które tworzą struktury graficzne. Graf składa się z zestawu wierzchołków, które są połączone krawędziami. Wierzchołki mogą reprezentować różne obiekty, takie jak miasta w sieci transportowej lub osoby w sieci społecznościowej. Ich znaczenie w teorii grafów polega na tym, że umożliwiają analizę i modelowanie złożonych relacji między obiektami. Zrozumienie roli wierzchołków jest kluczowe dla zastosowań w różnych dziedzinach, takich jak informatyka, matematyka, a nawet biologia.
Wierzchołki w grafach skierowanych i nieskierowanych: Kluczowe różnice
Grafy można podzielić na dwie główne kategorie: skierowane i nieskierowane. W grafach skierowanych, wierzchołki są połączone krawędziami, które mają określony kierunek. Oznacza to, że krawędź prowadzi od jednego wierzchołka do drugiego, co jest istotne w takich zastosowaniach jak analiza sieci społecznych, gdzie relacje mogą być jednostronne. Na przykład, w sieci Twittera, wierzchołki reprezentują użytkowników, a krawędzie wskazują, kto kogo obserwuje, co czyni ten graf skierowanym.
Z kolei w grafach nieskierowanych, wierzchołki są połączone krawędziami bez określonego kierunku. Oznacza to, że relacje między wierzchołkami są obustronne. Przykładem może być mapa drogowa, gdzie wierzchołki reprezentują miasta, a krawędzie wskazują drogi między nimi. W takim przypadku, podróż z jednego miasta do drugiego może odbywać się w obie strony, co czyni graf nieskierowanym. Zrozumienie tych różnic jest kluczowe dla analizy i modelowania różnych systemów.
- Sieci społecznościowe (skierowane) - relacje między użytkownikami mogą być jednostronne.
- Mapy drogowe (nieskierowane) - relacje między miastami są obustronne.
- Systemy rekomendacji (skierowane) - wierzchołki reprezentują użytkowników i przedmioty, a krawędzie wskazują preferencje.
Praktyczne zastosowania wierzchołków w informatyce i matematyce
Wierzchołki odgrywają kluczową rolę w wielu dziedzinach informatyki i matematyki, zwłaszcza w kontekście algorytmów i struktur danych. Na przykład w sieciach komputerowych wierzchołki reprezentują urządzenia, takie jak komputery lub routery, a krawędzie to połączenia między nimi. W aplikacjach takich jak optymalizacja tras, wierzchołki są używane do modelowania dróg i punktów docelowych, co pozwala na efektywne obliczanie najkrótszych tras. Algorytmy, takie jak Dijkstra, wykorzystują wierzchołki do znalezienia najkrótszej drogi w grafie, co jest niezwykle ważne w systemach nawigacyjnych.
Kolejnym przykładem zastosowania wierzchołków jest organizacja danych w bazach danych oraz w systemach rekomendacji. W takich systemach, wierzchołki reprezentują użytkowników oraz produkty, a krawędzie wskazują na preferencje i interakcje między nimi. Dzięki temu, algorytmy mogą analizować te relacje, aby rekomendować użytkownikom odpowiednie produkty. W rezultacie, wierzchołki są nie tylko fundamentalnym elementem teorii grafów, ale także mają praktyczne zastosowanie w codziennym życiu, wpływając na sposób, w jaki korzystamy z technologii.
| Algorytm | Opis | Zastosowanie |
|---|---|---|
| Dijkstra | Znajduje najkrótszą drogę w grafie z wierzchołkami i krawędziami | Systemy nawigacyjne, planowanie tras |
| Prim | Tworzy minimalne drzewo rozpinające w grafie | Optymalizacja sieci, budowa infrastruktury |
| Kruskal | Tworzy minimalne drzewo rozpinające, łącząc wierzchołki | Optymalizacja połączeń w sieciach |
Jak wierzchołki wpływają na rozwój sztucznej inteligencji i uczenia maszynowego
W miarę jak sztuczna inteligencja i uczenie maszynowe stają się coraz bardziej powszechne, zrozumienie roli wierzchołków w grafach staje się kluczowe dla rozwoju tych technologii. W kontekście analizy danych, wierzchołki mogą reprezentować różne cechy lub elementy w zbiorze danych, a krawędzie definiują relacje między nimi. Na przykład, w modelach rekomendacji, wierzchołki mogą być używane do reprezentowania użytkowników i produktów, a algorytmy mogą analizować te relacje, aby przewidzieć, co użytkownik może chcieć kupić. Dzięki temu, wierzchołki stają się fundamentem dla nowoczesnych systemów, które uczą się na podstawie danych i dostosowują swoje rekomendacje do indywidualnych potrzeb użytkowników.
Co więcej, wierzchołki odgrywają także istotną rolę w analizie sieci społecznych. W takich zastosowaniach, wierzchołki reprezentują osoby, a krawędzie wskazują na interakcje między nimi. Analizując te sieci, naukowcy mogą identyfikować kluczowe osoby wpływowe oraz zrozumieć, jak informacje rozprzestrzeniają się w sieci. W miarę jak technologia rozwija się, możemy spodziewać się, że wierzchołki będą odgrywać jeszcze większą rolę w modelowaniu złożonych systemów i rozwiązywaniu skomplikowanych problemów, takich jak przewidywanie trendów rynkowych czy optymalizacja procesów biznesowych.