Równanie to fundamentalny koncept w matematyce, który łączy dwa wyrażenia algebraiczne za pomocą znaku równości. W prostych słowach, równanie to zdanie matematyczne, które stwierdza, że dwie rzeczy są sobie równe. W tym artykule przyjrzymy się, czym dokładnie jest równanie, jakie są jego kluczowe elementy oraz jak je rozpoznać i analizować w praktyce.
Oprócz definicji, omówimy również różne rodzaje równań, takie jak równania liniowe i kwadratowe, oraz przedstawimy przykłady ich zastosowania w codziennym życiu. Zrozumienie równań jest kluczowe nie tylko w matematyce, ale także w wielu dziedzinach, takich jak fizyka, inżynieria czy ekonomia.
Najistotniejsze informacje:- Równanie to wyrażenie matematyczne, które łączy dwa terminy za pomocą znaku równości.
- Równania mają co najmniej jedną zmienną, która jest oznaczana literami i nazywana niewiadomą.
- Rozwiązywanie równań polega na znalezieniu wartości niewiadomych, które sprawiają, że równanie jest prawdziwe.
- Równania mogą być oznaczone (mają skończoną liczbę rozwiązań) lub nieoznaczone (mają nieskończoną liczbę rozwiązań).
- Przykłady równań można znaleźć w codziennym życiu, takie jak obliczenia kosztów czy pomiarów.
Równanie: Prosta definicja i podstawowe informacje
Równanie to fundamentalny element matematyki, który łączy dwa wyrażenia algebraiczne przy pomocy znaku równości. W prostych słowach, równanie jest zdaniem matematycznym, które stwierdza, że dwie wartości są sobie równe. Jest to kluczowy koncept, ponieważ pozwala na analizę i rozwiązywanie problemów matematycznych. W matematyce, równania mają różne zastosowania, od prostych obliczeń po bardziej złożone analizy w naukach przyrodniczych.Ważnym aspektem równań jest ich struktura. Równanie składa się z lewą stroną i prawą stroną, które są oddzielone znakiem równości. Zmienne w równaniach są oznaczane literami i nazywane są niewiadomymi. Zrozumienie, czym jest równanie, oraz jego podstawowych składników, stanowi fundament, na którym opiera się dalsza nauka matematyki.
Co to jest równanie? Zrozumienie podstawowych pojęć
Równanie to wyrażenie, które zawiera co najmniej jedną zmienną oraz stałe. W matematyce, służy ono do przedstawienia relacji między różnymi wartościami. Zmienne w równaniach to symbole, które reprezentują nieznane wartości, a ich rozwiązania to wartości, które spełniają dane równanie. Wartości te są określane jako dziedzina równania, co oznacza zbiór wszystkich możliwych wartości, które mogą być podstawione w miejsce niewiadomych.
- Równania są kluczowe w wielu dziedzinach, takich jak fizyka, inżynieria i ekonomia.
- Każde równanie ma swoją dziedzinę, która określa, jakie wartości można w nim zastosować.
- Rozwiązywanie równań polega na znalezieniu wartości niewiadomych, które sprawiają, że równanie jest prawdziwe.
Kluczowe elementy równania: Zmienne i wyrażenia algebraiczne
W każdym równaniu występują kluczowe elementy, które odgrywają istotną rolę w jego strukturze. Zmienne to symbole, które reprezentują nieznane wartości. Zazwyczaj oznaczane są literami, takimi jak x, y czy z. Oprócz zmiennych, równania zawierają także wyrażenia algebraiczne, które są kombinacjami zmiennych, stałych i operatorów matematycznych. Stałe to wartości, które nie zmieniają się, jak liczby całkowite czy ułamki.
Ważne jest zrozumienie, że lewa i prawa strona równania mogą zawierać różne wyrażenia algebraiczne, które po podstawieniu odpowiednich wartości zmiennych stają się równoważne. Dziedzina równania to zbiór wszystkich wartości, które można podstawić w miejsce zmiennych, aby równanie miało sens. Zrozumienie tych elementów jest kluczowe dla dalszej analizy i rozwiązywania równań.
Czytaj więcej: Co warto zobaczyć w Paryżu nocą – niezapomniane atrakcje i doświadczenia
Przykłady równań: Jak je rozpoznać i analizować
Równania można spotkać w wielu sytuacjach życiowych, a ich rozpoznawanie jest kluczowe dla zrozumienia otaczającego nas świata. Przykłady prostych równań to na przykład obliczenia związane z finansami, takie jak budżetowanie wydatków. Jeśli mamy równanie, które opisuje nasze wydatki jako sumę różnych kategorii, możemy łatwo zrozumieć, ile pieniędzy wydajemy na każdą z nich.
Kolejnym przykładem może być obliczanie odległości na podstawie prędkości i czasu. Równanie, które łączy te trzy zmienne, pozwala nam na szybkie określenie, jak daleko możemy podróżować w określonym czasie. Równania są zatem nie tylko narzędziem matematycznym, ale również praktycznym sposobem na podejmowanie decyzji w codziennym życiu.
- Obliczenia budżetowe: Równania pomagają w zarządzaniu wydatkami.
- Obliczenia odległości: Równania łączą prędkość, czas i dystans.
- Analiza danych: Równania mogą być używane w statystyce do modelowania zjawisk.
- Planowanie projektów: Równania pomagają w określaniu zasobów potrzebnych do realizacji zadań.
- Obliczenia w naukach przyrodniczych: Równania są kluczowe w fizyce i chemii do opisu reakcji i zjawisk.
Przykłady prostych równań: Zastosowanie w praktyce
Równania są obecne w wielu aspektach naszego codziennego życia i mają praktyczne zastosowania. Na przykład, jeśli planujesz zakup nowego samochodu, możesz użyć równania do obliczenia całkowitych kosztów, uwzględniając cenę zakupu, podatki i ubezpieczenie. Równanie może wyglądać tak: Całkowity koszt = Cena zakupu + Podatki + Ubezpieczenie.Kolejnym praktycznym zastosowaniem równań jest obliczanie dystansu. Na przykład, jeśli wiesz, że poruszasz się z prędkością 60 km/h przez 2 godziny, możesz użyć równania: Dystans = Prędkość × Czas, co daje 120 km. Takie równania pomagają w planowaniu podróży i określaniu czasu przybycia. Dzięki nim możemy podejmować bardziej świadome decyzje w codziennych sytuacjach.
Jak rozwiązywać równania? Krok po kroku do rozwiązania
Rozwiązywanie równań to proces, który wymaga kilku kroków. Po pierwsze, należy zidentyfikować równanie i określić, jakie zmienne są w nim obecne. Następnie, należy uporządkować równanie, aby wszystkie zmienne znalazły się po jednej stronie, a stałe po drugiej. W końcu, można przekształcić równanie, aby uzyskać wartość niewiadomej. Kluczowe jest, aby podczas tego procesu zachować równowagę, co oznacza, że każda operacja wykonana po jednej stronie musi być również wykonana po drugiej stronie równania.
Na przykład, rozważmy równanie 2x + 4 = 12. Aby je rozwiązać, zaczynamy od odjęcia 4 od obu stron: 2x = 8. Następnie dzielimy obie strony przez 2, aby uzyskać x = 4. Pamiętaj, aby zawsze sprawdzać swoje rozwiązanie, podstawiając je z powrotem do oryginalnego równania.
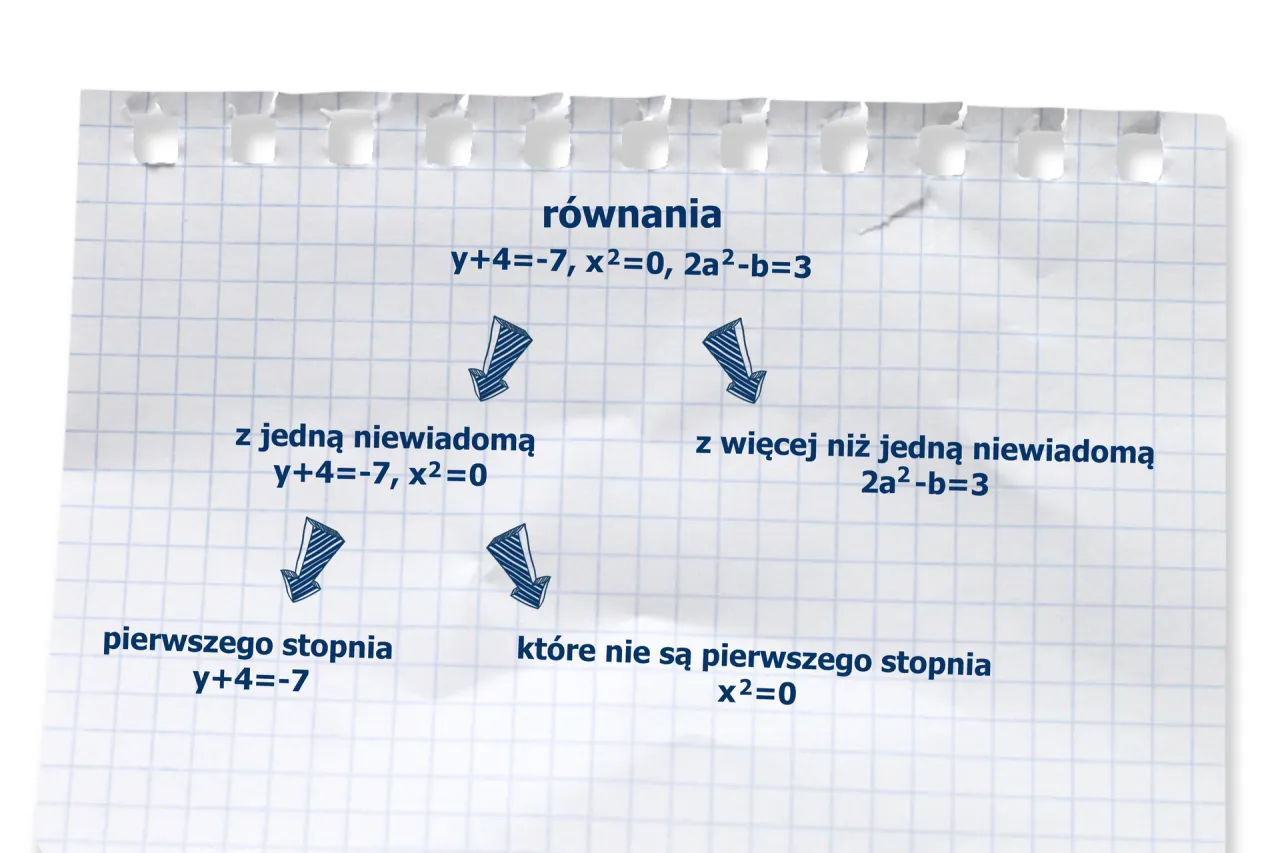
Rodzaje równań: Klasyfikacja i ich charakterystyka
Równania można klasyfikować na różne sposoby, w zależności od ich struktury i właściwości. Klasyfikacja równań jest istotna, ponieważ pozwala na lepsze zrozumienie ich funkcji oraz zastosowań w matematyce i innych dziedzinach. W matematyce wyróżniamy kilka głównych kategorii równań, które różnią się między sobą zarówno pod względem złożoności, jak i sposobu rozwiązywania.
Wśród najpopularniejszych rodzajów równań znajdują się równania liniowe, które przedstawiają relację prostoliniową między zmiennymi, oraz równania kwadratowe, które są bardziej złożone i zawierają zmienne podniesione do kwadratu. Inne typy to równania wielomianowe, które mogą mieć różne stopnie oraz równania różniczkowe, które są kluczowe w analizie matematycznej. Każdy z tych typów równań ma swoje unikalne cechy, które wpływają na ich zastosowanie w praktyce.
Równania liniowe: Definicja i przykłady z życia codziennego
Równania liniowe to równania, w których zmienne występują w pierwszej potędze i są połączone stałymi. Przykładem równania liniowego może być y = 2x + 3, gdzie y jest wartością zależną od x. Równania te są często stosowane w codziennym życiu, na przykład przy tworzeniu budżetu domowego, gdzie można obliczyć wydatki na podstawie różnych źródeł dochodu. Innym przykładem może być obliczanie odległości, gdzie równanie liniowe może opisywać relację między prędkością a czasem podróży.
Równania kwadratowe: Jak je rozpoznać i rozwiązać?
Równania kwadratowe to równania, w których zmienna występuje w drugiej potędze. Generalnie mają one postać ax² + bx + c = 0, gdzie a, b i c są stałymi, a x jest zmienną. Równania kwadratowe są istotne w wielu dziedzinach, w tym w fizyce, gdzie mogą opisywać ruch ciał w przestrzeni, na przykład w przypadku ruchu pocisków czy obiektów w trakcie swobodnego spadku. Dzięki swojej charakterystyce, równania kwadratowe mogą mieć dwa, jedno lub brak rozwiązań, w zależności od wartości współczynników a, b i c.
| Rodzaj równania | Charakterystyka | Przykład |
| Równania liniowe | Zmienne w pierwszej potędze, prostoliniowe | y = 2x + 3 |
| Równania kwadratowe | Zmienne w drugiej potędze, paraboliczne | y = x² - 4 |
Jak wykorzystać równania w codziennym podejmowaniu decyzji
Równania, w tym równania kwadratowe i liniowe, mogą być niezwykle przydatne w codziennym życiu, szczególnie w kontekście podejmowania decyzji finansowych i planowania. Na przykład, przy zakupie nieruchomości, można zastosować równania do obliczenia całkowitych kosztów kredytu hipotecznego, uwzględniając oprocentowanie oraz czas spłaty. Dzięki temu można lepiej zrozumieć, jakie będą miesięczne raty i jak wpływają one na całkowity budżet domowy.
Co więcej, w erze big data i analizy danych, umiejętność rozwiązywania równań staje się kluczowa. Firmy mogą wykorzystać równania do przewidywania trendów rynkowych, analizowania zachowań klientów oraz optymalizacji procesów. W miarę jak technologia się rozwija, narzędzia do modelowania matematycznego, w tym równania, będą odgrywać coraz większą rolę w podejmowaniu decyzji strategicznych w różnych branżach.

