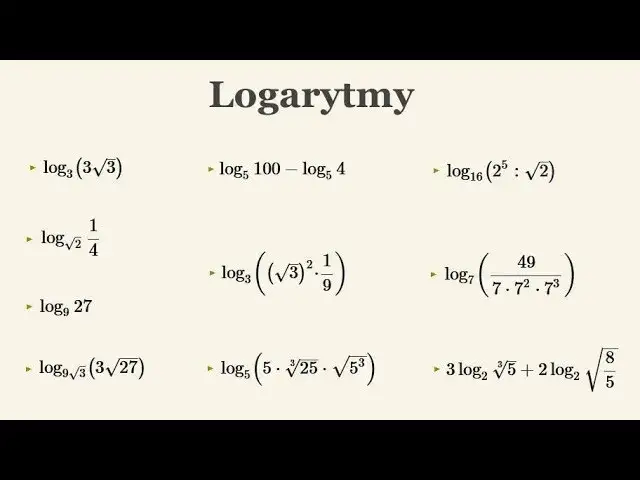Logarytmy to jedno z fundamentalnych pojęć matematycznych, które odgrywa kluczową rolę w rozwiązywaniu różnorodnych problemów, szczególnie tych związanych z potęgowaniem. Zrozumienie, jak działają logarytmy, jest istotne nie tylko w teorii, ale także w praktyce, ponieważ mają one zastosowanie w wielu dziedzinach, takich jak fizyka, chemia, ekonomia czy informatyka. W prostych słowach, logarytm odpowiada na pytanie: do jakiej potęgi trzeba podnieść podstawę, aby uzyskać daną liczbę? Na przykład, logarytm przy podstawie 2 z liczby 8 to 3, ponieważ 2 do potęgi 3 równa się 8.
W artykule przyjrzymy się nie tylko definicji logarytmów, ale także ich praktycznym zastosowaniom w codziennym życiu. Zrozumienie logarytmów może pomóc w uproszczeniu obliczeń, co jest szczególnie przydatne w sytuacjach, gdy mamy do czynienia z dużymi liczbami. Odkryjemy, jak logarytmy przyczyniają się do lepszego zrozumienia zjawisk w naukach ścisłych oraz jak są wykorzystywane w finansach i technologii.
Najistotniejsze informacje:- Logarytmy są kluczowym narzędziem w matematyce, pozwalającym na rozwiązywanie problemów związanych z potęgowaniem.
- Definicja logarytmu odnosi się do pytania, do jakiej potęgi trzeba podnieść podstawę, aby otrzymać daną liczbę.
- Logarytmy znajdują zastosowanie w różnych dziedzinach, takich jak fizyka, chemia, ekonomia i informatyka.
- W finansach logarytmy pomagają w obliczaniu procentu składanego, co jest kluczowe dla inwestycji.
- Logarytmy upraszczają obliczenia, zwłaszcza w przypadku dużych liczb, zamieniając mnożenie na dodawanie.
Logarytmy: Co to jest i dlaczego są ważne w matematyce?
Logarytmy to fundamentalne pojęcie w matematyce, które pozwala na rozwiązywanie problemów związanych z potęgowaniem. Definiują one, do jakiej potęgi należy podnieść daną podstawę, aby uzyskać określoną liczbę. Na przykład, logarytm przy podstawie 2 z liczby 8 wynosi 3, ponieważ 2 do potęgi 3 równa się 8. To narzędzie matematyczne jest nie tylko istotne w teorii, ale także w praktyce, ponieważ ma szerokie zastosowanie w różnych dziedzinach nauki.
W matematyce logarytmy odgrywają kluczową rolę w analizie i rozwiązywaniu złożonych problemów. Dzięki nim możemy uprościć obliczenia, szczególnie w sytuacjach, gdy mamy do czynienia z dużymi liczbami. Logarytmy są również niezbędne w naukach ścisłych, takich jak fizyka czy chemia, gdzie pomagają w opisie zjawisk, takich jak intensywność dźwięku czy reakcje chemiczne. Ich zrozumienie jest kluczowe dla każdego, kto chce zgłębiać tajniki matematyki i nauk przyrodniczych.
Definicja logarytmu i jego podstawowe właściwości
Logarytm to funkcja matematyczna, która odpowiada na pytanie, ile razy należy pomnożyć podstawę, aby uzyskać daną liczbę. Podstawowe właściwości logarytmów obejmują zasady dotyczące mnożenia, dzielenia oraz potęgowania. Na przykład, logarytm iloczynu dwóch liczb jest równy sumie logarytmów tych liczb (log(a * b) = log(a) + log(b)). Z kolei logarytm ilorazu dwóch liczb można wyrazić jako różnicę logarytmów (log(a / b) = log(a) - log(b)).
Inną ważną właściwością logarytmów jest zasada potęgowania, która mówi, że logarytm liczby podniesionej do potęgi jest równy iloczynowi tej potęgi i logarytmu liczby (log(a^b) = b * log(a)). Te podstawowe zasady sprawiają, że logarytmy są niezwykle przydatne w uproszczeniu skomplikowanych obliczeń matematycznych. Zrozumienie tych właściwości jest kluczowe dla dalszego zgłębiania bardziej zaawansowanych tematów w matematyce.
Dlaczego logarytmy są kluczowe w naukach ścisłych?
Logarytmy odgrywają niezwykle istotną rolę w różnych dziedzinach nauk ścisłych, takich jak fizyka, chemia oraz informatyka. W fizyce, logarytmy są używane do opisu zjawisk, takich jak intensywność dźwięku, gdzie skala decybeli opiera się na logarytmicznej skali pomiaru. W chemii, logarytmy pomagają w zrozumieniu reakcji chemicznych, zwłaszcza w kontekście pH, które jest logarytmiczną miarą stężenia jonów w roztworze.
W informatyce, logarytmy są kluczowe dla analizy złożoności algorytmów. Pomagają one w ocenie wydajności algorytmów, co jest niezbędne w programowaniu i rozwoju oprogramowania. Logarytmy pozwalają na uproszczenie obliczeń i lepsze zrozumienie struktury danych, co jest kluczowe dla efektywnego przetwarzania informacji.
Praktyczne zastosowania logarytmów w codziennym życiu
Logarytmy mają wiele praktycznych zastosowań w codziennym życiu, które są nie tylko teoretyczne, ale również bardzo użyteczne. W finansach, logarytmy pomagają w obliczaniu procentu składanego, co jest kluczowe dla inwestycji i zarządzania finansami osobistymi. W naukach przyrodniczych, logarytmy są stosowane do analizy danych, co pozwala na lepsze zrozumienie złożonych zjawisk.
- Logarytmy w finansach: obliczenia procentu składanego przy użyciu wzorów logarytmicznych.
- Logarytmy w chemii: zastosowanie w obliczeniach pH roztworów i ich wpływ na reakcje chemiczne.
- Logarytmy w fizyce: użycie w skali decybeli do pomiaru intensywności dźwięku.
| Przykład | Opis |
| Obliczanie pH | pH = -log10[H+], gdzie [H+] to stężenie jonów wodorowych. |
| Procent składany | A = P(1 + r/n)^(nt), gdzie A to wartość przyszła, P to kwota początkowa, r to stopa procentowa, n to liczba kapitalizacji rocznie, t to czas w latach. |
Logarytmy w finansach: jak obliczać procent składany?
Logarytmy odgrywają kluczową rolę w obliczaniu procentu składanego, co jest istotne w finansach osobistych oraz inwestycjach. Proces obliczania procentu składanego można zdefiniować za pomocą wzoru: A = P(1 + r/n)^(nt), gdzie A to wartość przyszła, P to kwota początkowa, r to roczna stopa procentowa, n to liczba kapitalizacji w roku, a t to czas w latach. Aby wyznaczyć czas, po jakim osiągniemy określoną wartość, możemy użyć logarytmu. Przykładowo, aby obliczyć, jak długo potrwa podwojenie inwestycji, możemy zastosować logarytm w równaniu 2P = P(1 + r/n)^(nt).
Logarytmy pozwalają na przekształcenie tego równania w formę, która umożliwia łatwiejsze obliczenia. Po przekształceniu, uzyskujemy równanie logarytmiczne, które możemy rozwiązać, aby znaleźć t. Dzięki temu, logarytmy stają się nieocenionym narzędziem w modelowaniu finansowym, pomagając inwestorom lepiej zrozumieć, jak ich pieniądze będą rosły w czasie.
| Kwota początkowa (P) | Stopa procentowa (r) | Czas (t) | Wartość przyszła (A) |
| 1000 zł | 5% | 10 lat | 1628,89 zł |
| 2000 zł | 3% | 15 lat | 3155,45 zł |
| 1500 zł | 4% | 20 lat | 3291,59 zł |
Zastosowanie logarytmów w naukach przyrodniczych i technice
Logarytmy znajdują również szerokie zastosowanie w naukach przyrodniczych i technice. W fizyce, na przykład, logarytmy są kluczowe w opisie intensywności dźwięku, gdzie stosuje się skalę decybeli, która jest logarymiczna. Dzięki temu, zmiany w intensywności dźwięku są bardziej zrozumiałe i proporcjonalne do percepcji ludzkiego ucha. W chemii, logarytmy są używane do obliczeń pH, które są logarymiczną miarą stężenia jonów wodorowych w roztworze, co jest istotne w wielu reakcjach chemicznych.
W technologii, logarytmy są stosowane w analizie danych oraz w algorytmach przetwarzania informacji. W informatyce, logarytmy pomagają w ocenie złożoności algorytmów, co jest kluczowe dla efektywności programów komputerowych. Zrozumienie tych zastosowań logarytmów pozwala na lepsze wykorzystanie ich w praktycznych sytuacjach, co czyni je niezbędnym narzędziem w wielu dziedzinach.
Czytaj więcej: Gdzie kupić Louis Vuitton Ombre Nomade? Sprawdź najlepsze opcje

Częste błędne przekonania o logarytmach i ich użyteczności
Wiele osób ma błędne przekonania na temat logarytmów, uważając je za skomplikowane i mało użyteczne narzędzie matematyczne. Często są postrzegane jako trudna matematyka, która nie ma zastosowania w codziennym życiu. W rzeczywistości logarytmy są niezwykle ważne, ponieważ pozwalają na uproszczenie złożonych obliczeń i pomagają w rozwiązywaniu problemów matematycznych. Ich zastosowanie w naukach ścisłych, finansach oraz technologii pokazuje, jak istotne są w zrozumieniu wielu zjawisk i procesów.
Logarytmy nie tylko ułatwiają obliczenia, ale również umożliwiają analizę danych w różnych dziedzinach. Umożliwiają one lepsze zrozumienie zjawisk, takich jak intensywność dźwięku czy skład chemiczny roztworów. Dlatego warto przełamać stereotypy i dostrzec, jak logarytmy mogą być użyteczne w życiu codziennym oraz w nauce.
Dlaczego logarytmy nie są tylko „trudną matmą”?
Logarytmy często są postrzegane jako trudne, co może wynikać z ich abstrakcyjnej natury. Jednak zrozumienie ich podstawowych zasad nie musi być skomplikowane. Kluczem do łatwiejszego przyswajania logarytmów jest praktyka oraz zastosowanie ich w konkretnych sytuacjach. Warto zacząć od prostych przykładów, które pomogą zbudować pewność siebie i zrozumienie tej matematyki.
Jednym ze sposobów na przezwyciężenie trudności jest korzystanie z wizualizacji i narzędzi online, które ilustrują, jak logarytmy działają w praktyce. Dzięki temu, uczniowie mogą zobaczyć, jak logarytmy są używane w rzeczywistych problemach, co czyni je bardziej przystępnymi. W ten sposób można zrozumieć, że logarytmy są nie tylko narzędziem matematycznym, ale również praktycznym wsparciem w codziennym życiu.
Jak logarytmy upraszczają skomplikowane obliczenia?
Logarytmy są potężnym narzędziem, które upraszczają skomplikowane obliczenia, szczególnie w kontekście mnożenia i dzielenia. Dzięki właściwościom logarytmów, możemy zamienić operacje mnożenia na dodawanie, co znacznie ułatwia obliczenia. Na przykład, zamiast mnożyć duże liczby, możemy dodać ich logarytmy, a następnie przekształcić wynik z powrotem na formę liczbową. To podejście jest szczególnie przydatne w sytuacjach, gdy mamy do czynienia z dużymi wartościami, co może być czasochłonne i podatne na błędy, gdy wykonujemy obliczenia ręcznie.
Logarytmy pozwalają również na uproszczenie dzielenia, które możemy zamienić na odejmowanie logarytmów. Dzięki temu, złożone obliczenia stają się bardziej przystępne i mniej czasochłonne. Użycie logarytmów w obliczeniach nie tylko zwiększa efektywność, ale także zmniejsza ryzyko popełnienia błędów, co jest kluczowe w matematyce i naukach ścisłych. Warto zatem zrozumieć, jak logarytmy mogą być używane do uproszczenia obliczeń, co czyni je nieocenionym narzędziem w codziennym życiu.
Jak logarytmy wspierają rozwój umiejętności analitycznych?
Logarytmy nie tylko upraszczają obliczenia, ale również wspierają rozwój umiejętności analitycznych, które są niezbędne w dzisiejszym świecie. Zrozumienie logarytmów pozwala na lepsze przyswajanie koncepcji matematycznych oraz rozwijanie zdolności do analizy danych. W miarę jak technologia staje się coraz bardziej złożona, umiejętność myślenia analitycznego, w tym umiejętność korzystania z logarytmów, staje się kluczowa w wielu dziedzinach, takich jak programowanie, finanse czy nauki przyrodnicze.
W praktyce, umiejętność stosowania logarytmów w analizie danych może prowadzić do bardziej efektywnego podejmowania decyzji. Na przykład, w analizie statystycznej, logarytmy są używane do transformacji danych, co pozwala na lepsze zrozumienie rozkładów i identyfikację trendów. W przyszłości, z rosnącym znaczeniem danych i analityki w biznesie, umiejętność wykorzystywania logarytmów może stać się kluczowym atutem na rynku pracy, otwierając drzwi do nowych możliwości zawodowych i rozwoju kariery.